Classification
Table of contents
Introduction
Classification is a basic concept in machine learning where we categorize data into predefined classes or labels. For example, an email might be classified as “spam” or “not spam,” and a medical image could be classified as showing “cancerous” or “non-cancerous” tissue.
Definition of Classification
The Classification is the task of mapping from a feature space to a label space. The goal is to learn a function $\mathcal{P}$ that maps features to labels. This function is called the Prediction Function or Prediction Strategy or Inference Rule.
\[\mathcal{P}: \mathcal{X} \rightarrow \mathcal{Y}\] \[\mathcal{P}(\boldsymbol{x}) = y, \quad \boldsymbol{x} \in \mathcal{X}, \quad y \in \mathcal{Y}\]
For this course Classification is the process of mapping from a feature space $\mathbb{R}^{d}$ to a label space $\mathbb{N}$. The task is to learn a prediction function $\mathcal{P}$ that creates a prediction $\hat{y}$ from the feature vector $\boldsymbol{x}$ and we want the prediction to be as close as possible to the true label $y$.
\[\mathcal{P}(\boldsymbol{x}) = \hat{y}, \quad \boldsymbol{x} \in \mathbb{R}^{d}, \quad \hat{y} \in \mathbb{N}\]
This can be visualized as the following schematic:
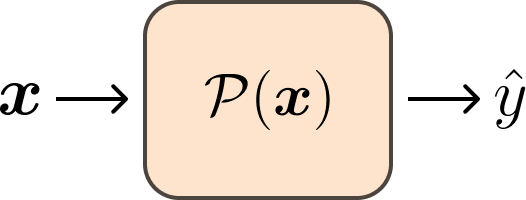
Logits and Scores
As we previously discussed, a classifier can be viewed as a function that maps features to corresponding labels. However, this approach can sometimes be limiting when we want to understand the confidence of our predictions.
To address this, we introduce the concept of logits or scores (\(\boldsymbol{s}\)).
The logits / scores $\boldsymbol{s}$ is a vector of length $c$, where $c$ is the number of classes. It quantifies the classifier’s confidence in each class. The elements of $\boldsymbol{s}$ represent the degree of certainty or score associated with each class, indicating how strongly the classifier leans towards each possible classification outcome. The logits are then used for prediction, where the class with the highest score is the predicted class.
The terms logits and scores are often used interchangeably, though they can have slightly different connotations depending on the context:
- Logits: This term is frequently used in the context of neural networks, particularly in the final layer of a classification model. Logits are the raw, unnormalized scores output by a neural network. These scores are typically transformed into probabilities using a function like softmax.
- Scores / Score Vector: This term is more general and can refer to any vector of scores or confidences that a classifier assigns to different classes. It doesn’t necessarily imply that the scores are unnormalized, though it often does. The score vector could be the direct output of a model or the result of some intermediate computation.
In this course, we will primarily use the term logits, as it is more commonly used in the context of neural networks.
Modification of the Prediction Function
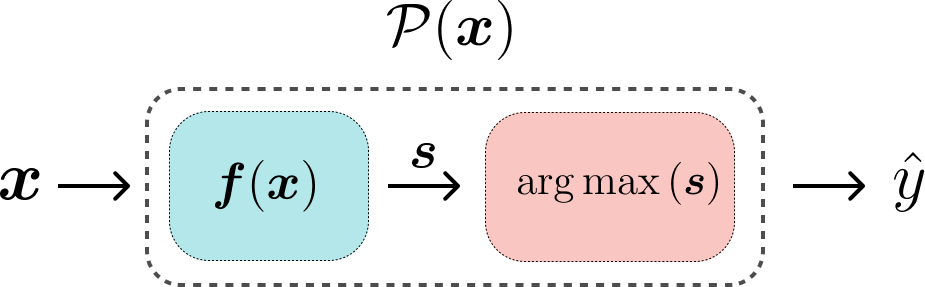
With this understanding, we can modify our classification task to include an intermediate step involving logits. Every classifier, whether it’s a simple k-Nearest Neighbors or a complex neural network, has some form of logits inside its prediction function. This step is crucial, so we define a new function $\boldsymbol{f}$ that returns the logits $\boldsymbol{s}$:
\[\boldsymbol{f}: \mathbb{R}^{d} \rightarrow \mathbb{R}^{c}\] \[\boldsymbol{f}(\boldsymbol{x}) = \boldsymbol{s}, \quad \boldsymbol{x} \in \mathbb{R}^{d}, \quad \boldsymbol{s} \in \mathbb{R}^{c}\]This function maps a feature vector $\boldsymbol{x}$ to a logits vector $\boldsymbol{s}$. The prediction is then made by selecting the class with the highest logit value:
\[\hat{y} = \arg\max \boldsymbol{s}\]Thus, our original prediction function \(\mathcal{P}(\boldsymbol{x})\) can now be understood as a two-step process: \(\mathcal{P}(\boldsymbol{x}) = \arg\max(\boldsymbol{f}(\boldsymbol{x}))\).
The relationship between the logits $\boldsymbol{s}$ and the class prediction $\hat{y}$ can be visualized as follows:
Expected Knowledge
Answer the following questions to test your understanding of the classification task.
-
Logits vs. Labels: What is the primary advantage of designing a classifier to output a vector of logits \(\boldsymbol{s}\) instead of directly outputting a final class label \(\hat{y}\)? Provide a robotics-related example where this advantage would be critical for safe or effective operation.
- From Logits to Prediction: A classifier is designed to sort fruit into three classes: {0: ‘apple’, 1: ‘banana’, 2: ‘cherry’}. For a given image, the model’s internal function \(\boldsymbol{f}\) produces the logits vector \(\boldsymbol{s} = [1.5, 4.1, -0.2]\).
- What is the final predicted class index \(\hat{y}\)?
- Which fruit does the model predict?
- Explain mathematically how you arrived at this prediction.
- Formal Definitions: In your own words, explain the difference between the feature space \(\mathcal{X}\) and the label space \(\mathcal{Y}\) in a classification problem. Why is the mapping for classification typically from \(\mathbb{R}^d\) to \(\mathbb{N}\)?